文章目录
一、猴子摘香蕉问题
1、问题描述
利用一阶谓词逻辑求解猴子摘香蕉问题:房内有一个猴子,一个箱子,天花板上挂了一串香蕉,其位置如图1所示,猴子为了拿到香蕉,它必须把箱子搬到香蕉下面,然后再爬到箱子上。请定义必要的谓词,列出问题的初始化状态(即下图所示状态),目标状态(猴子拿到了香蕉,站在箱子上,箱子位于位置b)。 (附加:从初始状态到目标状态的谓词演算过程。)

2、解题思路
猴子按照先到箱子所在位置/从箱子上爬下来→把箱子搬到香蕉下面→爬上箱子摘香蕉的逻辑进行着。 所以需要编写四个行动逻辑——走到箱子所在位置、从箱子上爬下来、把箱子搬到香蕉上面、爬上箱子摘香蕉。
使用一个结构定义猴子、箱子、香蕉、相对箱子的位置状态—— 猴子在A点则标-1,猴子在B点则标0,猴子在C点则标1 箱子在A点则标-1,箱子在B点则标0,箱子在C点则标1 香蕉在A点则标-1,香蕉在B点则标0,香蕉在C点则标1 猴子爬上箱子则标1,没爬上则标-1
struct State
{
int monkey; /*-1:Monkey at A;0: Monkey at B;1:Monkey at C;*/
int Box; /*-1:Box at A;0:Box at B;1:Box at C;*/
int banana; /*Banana at B,Banana=0*/
int monBox; /*-1: monkey on the Box;1: monkey the Box;*/
};
struct State States[150];输入一个初始状态(a, b, c, d) 根据问题,确定终止状态是猴子摘到香蕉{(x,x,x,0)}(x 属于 {0,-1, 1})。
使用递归调用的方式搜索路径,每次递归前先判断当前状态是否与之前的状态重复,若重复则认为形成一个环路,回到上一步寻找其他方式通往新的状态。
3、实验结果及分析
实验结果一

分析: 初始时,猴子站在A位置,箱子在C位置,香蕉在B位置,猴子没有站在箱子上。
猴子摘香蕉的步骤如下: 猴子走去C位置→猴子把箱子从C位置搬到B位置→猴子爬上箱子→猴子摘到香蕉
实验结果二
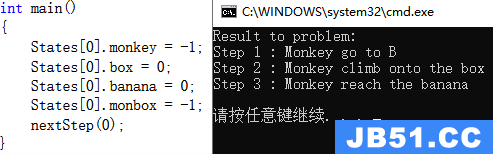
分析: 初始时,猴子站在A位置,箱子在B位置,香蕉在B位置,猴子没有站在箱子上。
猴子摘香蕉的步骤如下: 猴子走去B位置→猴子爬上箱子→猴子摘到香蕉
实验结果三
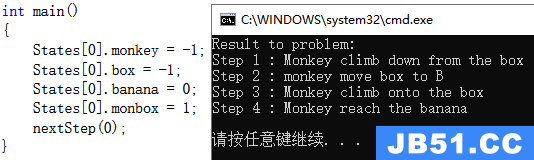
分析: 初始时,猴子站在A位置,箱子在A位置,香蕉在B位置,猴子站在箱子上。
猴子摘香蕉的步骤如下: 猴子从箱子上爬下来→猴子把箱子从A位置搬到B位置→猴子爬上箱子→猴子摘到香蕉
4、实验结果
当传教士与野人为五人,船最多允许三人过河时,程序运行结果如下
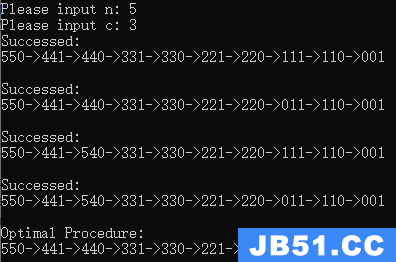
解的状态迁移图 1、550->441->440->331->330->221->220->111->110->001
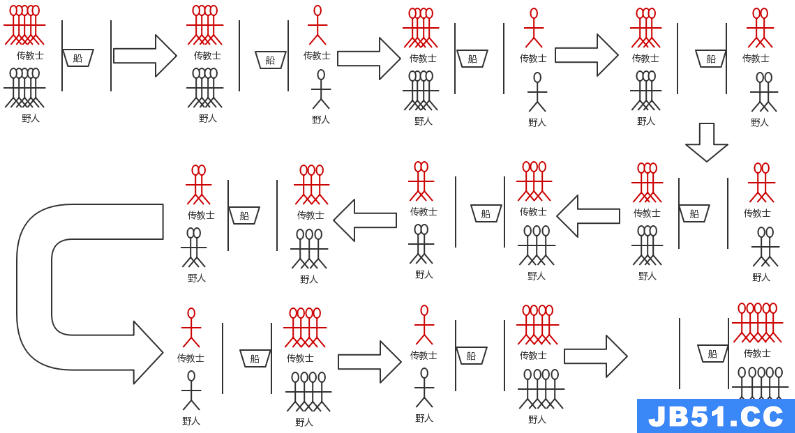
2、550->441->440->331->330->221->220->011->110->001
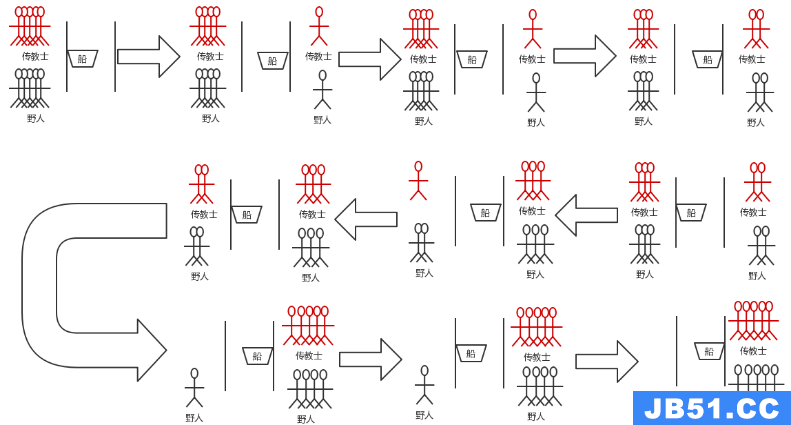
3、550->441->540->331->330->221->220->111->110->001

4、550->441->540->331->330->221->220->011->110->001

5、实验代码
#include "stdafx.h"
#include<string.h>
#include<iostream>
#include <stdio.h>
using namespace std;
struct State
{
int monkey; /*-1:Monkey at A;0: Monkey at B;1:Monkey at C;*/
int Box; /*-1:Box at A;0:Box at B;1:Box at C;*/
int banana; /*Banana at B,Banana=0*/
int monBox; /*-1: monkey on the Box;1: monkey the Box;*/
};
struct State States[150];
char* routesave[150];
/*function monkeygoto,it makes the monkey goto the other place*/
void monkeygoto(int b, int i)
{
int a;
a = b;
if (a == -1)
{
routesave[i] = "Monkey go to A";
States[i + 1] = States[i];
States[i + 1].monkey = -1;
}
else if (a == 0)
{
routesave[i] = "Monkey go to B";
States[i + 1] = States[i];
States[i + 1].monkey = 0;
}
else if (a == 1)
{
routesave[i] = "Monkey go to C";
States[i + 1] = States[i];
States[i + 1].monkey = 1;
}
else
{
printf("parameter is wrong");
}
}
/*end function monkeyygoto*/
/*function moveBox,the monkey move the Box to the other place*/
void moveBox(int a, int i)
{
int B;
B = a;
if (B == -1)
{
routesave[i] = "monkey move Box to A";
States[i + 1] = States[i];
States[i + 1].monkey = -1;
States[i + 1].Box = -1;
}
else if (B == 0)
{
routesave[i] = "monkey move Box to B";
States[i + 1] = States[i];
States[i + 1].monkey = 0;
States[i + 1].Box = 0;
}
else if (B == 1)
{
routesave[i] = "monkey move Box to C";
States[i + 1] = States[i];
States[i + 1].monkey = 1;
States[i + 1].Box = 1;
}
else
{
printf("parameter is wrong");
}
}
/*end function moveBox*/
/*function climbonto,the monkey climb onto the Box*/
void climbonto(int i)
{
routesave[i] = "Monkey climb onto the Box";
States[i + 1] = States[i];
States[i + 1].monBox = 1;
}
/*function climbdown,monkey climb down from the Box*/
void climbdown(int i)//如果初始状态猴子在箱子上,则需要爬下来
{
routesave[i] = "Monkey climb down from the Box";
States[i + 1] = States[i];
States[i + 1].monBox = -1;
}
/*function reach,if the monkey,Box,and banana are at the same place,the monkey reach banana*/
void reach(int i)
{
routesave[i] = "Monkey reach the banana";
}
/*output the solution to the problem*/
void showSolution(int i)//打印
{
int c;
printf("%s \n", "Result to problem:");
for (c = 0; c<i + 1; c++)
{
printf("Step %d : %s \n", c + 1, routesave[c]);
}
printf("\n");
}
/*perform next steP*/
void nextStep(int i)
{
int c;
int j;
//超过一定步数,判断为有问题
if (i >= 150)
{
printf("%s \n", "steplength reached 150,have problem ");
return;
}
//判断是否跟之前的状态相同,若相同则可能陷入循环,需要退出
for (c = 0; c<i; c++) /*if the current state is same to prevIoUs,retrospect*/
{
if (States[c].monkey == States[i].monkey&&States[c].Box == States[i].Box&&States[c].banana == States[i].banana&&States[c].monBox == States[i].monBox)
return;
}
//成功拿到香蕉
if (States[i].monBox == 1 && States[i].monkey == 0 && States[i].banana == 0 && States[i].Box == 0)
{
showSolution(i);
exit(0);
}
j = i + 1;//进行数据更新,用来标记当前是第几个状态
if (States[i].monkey == 0)//猴子站在了位置0
{
if (States[i].Box == 0)
{
if (States[i].monBox == -1)
{
climbonto(i);
reach(i + 1);
nextStep(j);
}
else
{
reach(i + 1);
nextStep(j);
}
}
else
{
monkeygoto(States[i].Box, i);
nextStep(j);
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
}
/*end if*/
if (States[i].monkey == -1)
{
if (States[i].Box == -1)
{
if (States[i].monBox == -1)
{
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
else
{
climbdown(i);
nextStep(j);
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
}
else if (States[i].Box == 0)
{
monkeygoto(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
else
{
monkeygoto(1, i);
nextStep(j);
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
}
/*end if*/
if (States[i].monkey == 1)
{
if (States[i].Box == 1)
{
if (States[i].monBox == -1)
{
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
else
{
climbdown(i);
nextStep(j);
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
}
else if (States[i].Box == -1)
{
monkeygoto(-1, i);
nextStep(j);
moveBox(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
else
{
monkeygoto(0, i);
nextStep(j);
climbonto(i);
reach(i + 1);
nextStep(j);
}
}
/*end if*/
}/*end nextSteP*/
int main()
{
States[0].monkey = -1;
States[0].Box = 1;
States[0].banana = 0;
States[0].monBox = -1;
nextStep(0);
}二、传教士(牧师)与野人问题
1、问题描述
有n个牧师和n个野人准备渡河,但只有一条能容纳c个人的小船,为了防止野人侵犯牧师,要求无论在何处,牧师的人数不得少于野人的人数(除非牧师人数为0),且假定野人与牧师都会划船,试设计一个算法,确定他们能否渡过河去,若能,则给出小船来回次数最少的最佳方案。
2、实验步骤
输入:牧师人数(即野人人数):n;小船一次最多载人量:c。 输出:若问题无解,则显示Failed,否则,显示Successed输出所有可行方案,并标注哪一组是最佳方案。用三元组(X1, X2, X3)表示渡河过程中的状态。并用箭头连接相邻状态以表示迁移过程:初始状态->中间状态->目标状态。
例:当输入n=2,c=2时,输出:221->200->211->010->021->000; 其中:X1表示起始岸上的牧师人数;X2表示起始岸上的野人人数;X3表示小船现在位置(1表示起始岸,0表示目的岸)。
3、实验要求
写出算法的设计思想和源程序,并有用户界面实现人机交互(控制台或者窗口都可以),进行输入和输出结果,如: Please input n: 2 Please input c: 2 Optimal Procedure: 221->200->211->010->021->000 Successed or Failed?: Successed
4、解题思路
针对“传教士与野人”实验,输入不同的传教士与野人数目,允许过河的最大人数,可以得到不同的结果。在输出所有可行路径之后,输出最优路径,即所花次数最少的结果。 这题使用DFS算法,运用递归来写DFS算法,搜索扫描可能的路径,若可行则打印出来,同时比较当前路径是否比已存储的最短路径短,若是,则当前路径存储为最短路径,若否则跳过。
5、实验代码
// 传教士与野人.cpp
#include <iostream>
using namespace std;
#define maxnum 150
struct op
{
int M; //牧师过河人数
int C; //野人过河人数
};
struct State
{
int minister; //起始岸上的牧师人数
int savage; //起始岸上的野人人数
int side; //side=0,船在初始岸,side=1,船在对岸
};
int n; //牧师和野人数目
int c; //小船最多能载的人数
int op_num; //有多少种过河方式
int min_road=999;//最短路径
struct op opNum[maxnum];
struct State States[maxnum];
struct State StatesMin[maxnum];
//安全状态
int isSafe(int i)
{
if (States[i].minister == 0 || States[i].minister == n || States[i].minister == States[i].savage)
return 1;
return 0;
}
//最终目标
int isGoal(int i)
{
if (States[i].minister == 0 && States[i].savage == 0)
return 1;
return 0;
}
//判断是否跟之前的状态重复
int isRepeat(int i)
{
for (int j = 0; j < i; j++)
{
if (States[i].minister == States[j].minister&&States[i].savage == States[j].savage&&States[i].side==States[j].side)
return 1;
}
return 0;
}
//可选择的过河方式
void OpNum()
{
for(int i=0;i<=c;i++)
for (int j = 0; j <= i&&j<=c-i; j++)
{
opNum[op_num].M = i;
opNum[op_num++].C = j;
}
}
//存储最短的过河方式
void MinWay(int i)
{
for (int j = 0; j <= i; j++)
{
StatesMin[j].minister = States[j].minister;
StatesMin[j].savage = States[j].savage;
StatesMin[j].side = States[j].side;
}
}
//打印
void Print(State *state,int i)
{
for (int j = 0; j < i; j++)
{
cout << state[j].minister << state[j].savage << state[j].side<<"->";
if (j + 1 % 10 == 0)
cout << endl;
}
cout << state[i].minister << state[i].savage << state[i].side <<endl<<endl;
}
//使用dfs遍历寻找解
void nextStep(int i)
{
// 递归出口
if (isGoal(i))
{
if (i < min_road)
{
min_road = i;
MinWay(i);
}
cout << "Successed:" << endl;
Print(States,i);
return;
}
// 是否安全
if (!isSafe(i))
return;
// 是否重复
if (isRepeat(i))
return;
int j = i + 1;
// 起始岸
if (States[i].side == 0)
{
for (int k = 0; k < op_num; k++)
{
if (opNum[k].M > States[i].minister || opNum[k].C > States[i].savage)
continue;
States[j].minister = States[i].minister-opNum[k].M;
States[j].savage = States[i].savage - opNum[k].C;
States[j].side = 1;
nextStep(j);
}
}
else//对岸
{
for (int k = 0; k < op_num; k++)
{
if (opNum[k].M > (n-States[i].minister) || opNum[k].C > (n-States[i].savage))
continue;
States[j].minister = States[i].minister+opNum[k].M;
States[j].savage = States[i].savage+opNum[k].C;
States[j].side = 0;
nextStep(j);
}
}
}
int main()
{
cout << "Please input n: ";
cin >> n;
cout << "Please input c: ";
cin >> c;
States[0].minister = n;
States[0].savage = n;
States[0].side = 0;
OpNum();
nextStep(0);
if (min_road < 999)
{
cout << "Optimal Procedure:" << endl;
Print(StatesMin, min_road);
}
else
{
cout << "Fail." << endl;
}
return 0;
}版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




