浙大数据结构学习之基本概念 1

一.实例

 

到100000时递归不再运行程序，原因是内存超限。

 

 

秦九韶法优化

 

 下面开始测时间。

 

发现时间太短测不出来，重复后除以次数。 

 

 

 

讨论1.3 再试一个多项式

老师参与

给定另一个100阶多项式

，用不同方法计算并且比较一下运行时间？

 

#include <stdio.h>
#include <time.h>
#include <math.h>
double f1(int n,double a[],double x);
double f2(int n,double a[],double x);
clockid_t strat,stop;
double duration;
#define MAXN 101
int main(){
	double a[MAXN];
	for(int i=1;i<MAXN;i++){
		if(i==0){
			a[i]=1.0;
		}
		else{
		a[i]=1.0/i;	
		}
	}
	strat=clock();
	for(int i=0;i<1000000;i++)
	f1(MAXN-1,a,1.2);
    stop=clock();
    duration=((double)(strat-stop))/CLK_TCK/10000;
    printf("第一个算法的耗时：%f",duration);
   strat=clock();
   	for(int i=0;i<1000000;i++)
   	f2(MAXN-1,a,1.2);
    stop=clock();
    duration=((double)(strat-stop))/CLK_TCK/10000;
    printf("第二个算法的耗时：%f",duration);
    
    
	
	



	
	
	
}
double f1(int n,double a[],double x){
	
	double p=0;
	for(int i=0;i<=n;i++){
		p+=a[i]*pow(x,i);
	}
	return p;
}

double f2(int n,double a[],double x){
	double p=a[n];
	for(int i=n;i>=1;i--){
		p=a[i-1]+x*p;
	}
	return p;
	
	
}

二.数据结构：

 

 

 

 三.算法

 

 

 

注意：

 

 

 

 

要找最小的上界和最大的下界

下面介绍一下时间复杂度上界和下界：

 

 

（1）大O记号(渐近上界记号)

定义1-1  

设函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在两个正常数c和n0，使得当n≥n0时，有f(n)≤cg(n)，则记做f(n) = O(g(n))，称为大O记号（big Oh notation） 称g(n)是f(n)的一个上界 注： f(n)的阶不高于g(n)

例1-1   f(n) = 2n + 3 = O(n)

当n≥3时，2n+3≤3n，

所以，可选c = 3，n0 = 3。对于n≥n0，f(n) = 2n + 3≤3n，

所以， f(n) = O(n) 。这意味着，当n≥3时，该程序步不会超过3n。

例1-2  f(n) = 10n2 + 4n + 2 = O(n2)

对于n≥2时，有10n2 + 4n + 2≤10n2 + 5n，

并且当n≥5时，5n≤n2， 因此，可选c = 11, n0 = 5；

对于n≥n0，f(n) = 10n2 + 4n + 2≤11n2， 所以f(n) = O(n2)。

例1-3 10n2 + 9 ！=O(n)

使用反证法，假定存在c和n0，使得对于n≥n0，10n2 + 9≤cn始终成立，

那么有10n + 9/n≤c，即n≤c/10 - 9/(10n)总成立。

但此不等式不可能总成立，取n = c/10 + 1时，该不等式便不再成立。

重要定理

渐近时间复杂度    

使用大O记号及下面定义的几种渐近表示法表示的算法时间复杂度，

称为算法的渐近时间复杂度（asymptotic complexity），简称时间复杂度

适当选择关键操作，算法的渐近时间复杂度可以由关键操作的执行次数之和来计算

一般地，关键操作的执行次数与问题的规模有关，是n的函数

【程序1-4】  矩阵乘法

1. for（i=0; i<n; i++） //n+1

2. for（j=0; j<n; j++）{ //n(n+1)

3. c[i][j]=0; //n2

4. for（k=0; k<n; k++） //n2(n+1)

5. c[i][j]+=a[i][k]*b[k][j]; //n3

6. }

总的时间： n3+ n2(n+1)+ n2+ n(n+1)+ n+1 =2n3+3n2+2n+1   渐进时间复杂度：O(n3)

 
大O运算规则:

(1) O(f)+O(g)=O(max(f, g))
(2) O(f)+O(g)=O(f+g)
(3) O(f)O(g)=O(fg)
(4) 如果g(N)=O(f(N)), 则O(f)+O(g)=O(f)
(5) O(Cf(N))=O(f(N)), 其中C是一个正常数
(6) f=O(f)

（2）Ω记号(渐近下界记号)

定义2-2    设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在两个正常数 c和n0，使得当n≥n0时，有f(n)≥c g(n)，则记做f(n) = Ω (g(n))，称为Ω记号（omega notation）。 注： f(n)的阶不低于g(n)

（Ω的相关概念实际上就是O（n）颠倒过来）

例1-5  f(n) = 2n + 3 =Ω(n)

对所有n，2n+3≥2n，可选c = 2，n0=0。

对于n≥n0，f(n) = 2n+3≥2n，所以，f(n) = Ω(n)，即2n + 3∈Ω(n)。

例1-6  f(n) = 10n2 + 4n + 2 = Ω(n2)

对所有n，10n2 + 4n + 2≥10n2，可选c = 10，n0 = 0。

对于n≥n0，f(n) = 10n2 + 4n + 2≥10n2，所以，f(n) =Ω(n^2)。

重要定理

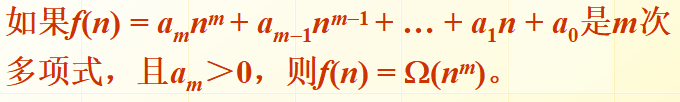
（3） θ记号（紧渐近界记号）

定义1-3 设有函数f(n)和g(n)是定义在非负整数集合上的正函数，如果存在正常数c1，c2和n0，使得当n≥n0时，有c1 g(n)≤f(n)≤c2 g(n)，则记做f(n) = θ(g(n))，称为θ记号（Theta notation）。 注：此时f(n)和g(n)同阶

例1-7  f(n) = 2n + 3 = θ(n)

例1-8  f(n) = 10n2 + 4n + 2 = θ(n^2)

（4）算法按时间复杂度分类

多项式时间算法

凡渐近时间复杂度有多项式时间限界的算法称做多项式时间算法（polynomial time algorithm）

O(1)＜O(log n)＜O(n)＜O(nlog n)＜O(n^2)＜O(n^3)

指数时间算法

渐近时间复杂度为指数函数限界的算法称做指数时间算法（exponential time algorithm）

O(2^n)＜O(n!)＜O(n^n)

时间复杂度增长示意图

判断时间复杂度是否为准确值相关定理

如果存在正常数n0, 使得当n≥n0时有f(n)>0, g(n)>0

并且  

  则f(n)=O(g(n))

如果存在正常数n0, 使得当n≥n0时有f(n)>0, g(n)>0

并且  

 则f(n)=θ(g(n))

书上相关例题参考答案：

函数的输入规模：

 

四.实例感悟

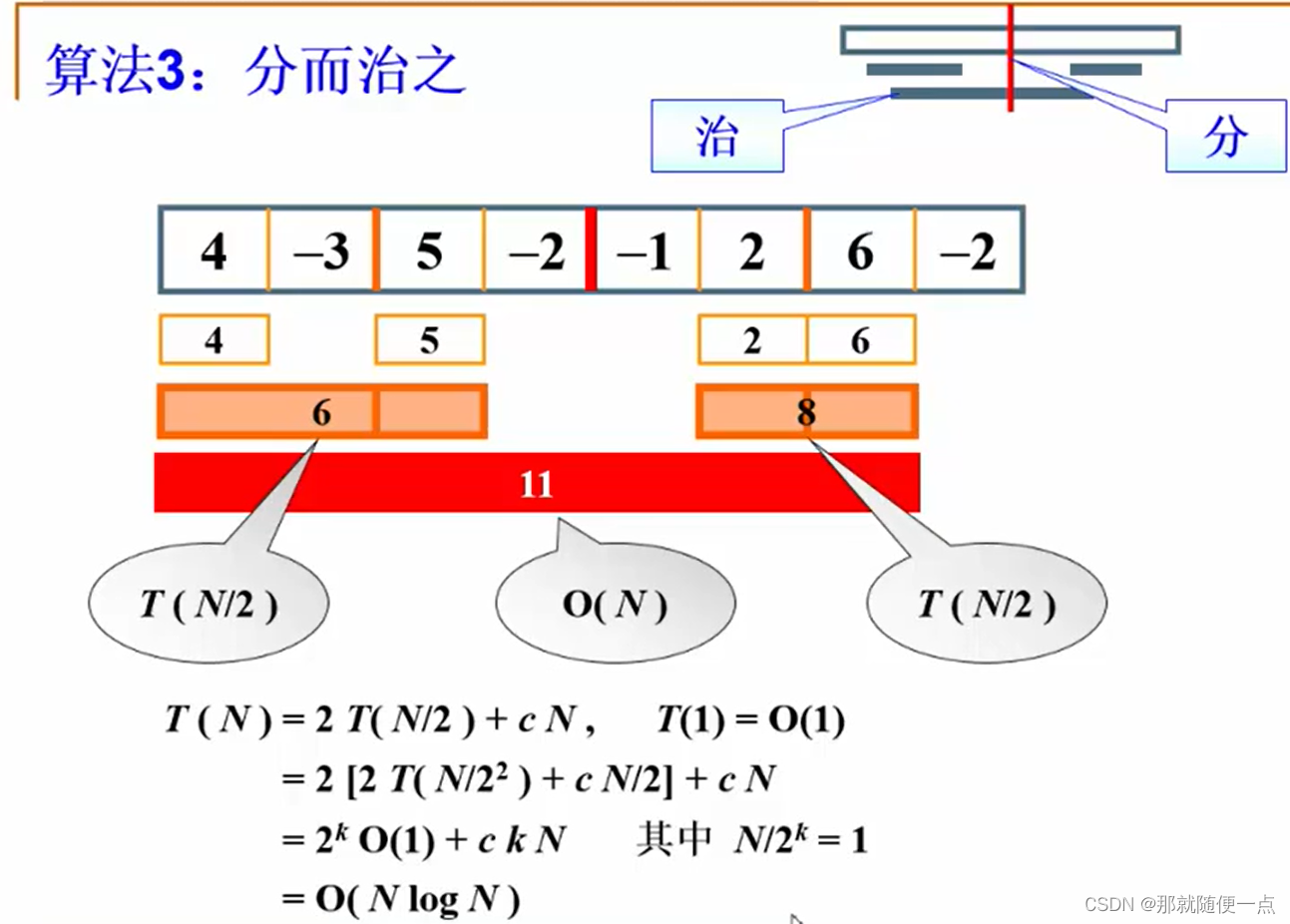
int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}

int DivideAndConquer( int List[], int left, int right )
{ /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/

    int LeftBorderSum, RightBorderSum;
    int center, i;

    if( left == right )  { /* 递归的终止条件，子列只有1个数字 */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }

    /* 下面是"分"的过程 */
    center = ( left + right ) / 2; /* 找到中分点 */
    /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );

    /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */

    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */

    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}

int MaxSubseqSum3( int List[], int N )
{ /* 保持与前2种算法相同的函数接口 */
    return DivideAndConquer( List, 0, N-1 );
}

 

 

 

 

原文地址：https://www.jb51.cc/wenti/3280011.html