99-恢复二叉搜索树

二叉搜索树的概念：
根节点要小于右子树的节点，必须要大于左子树的节点。

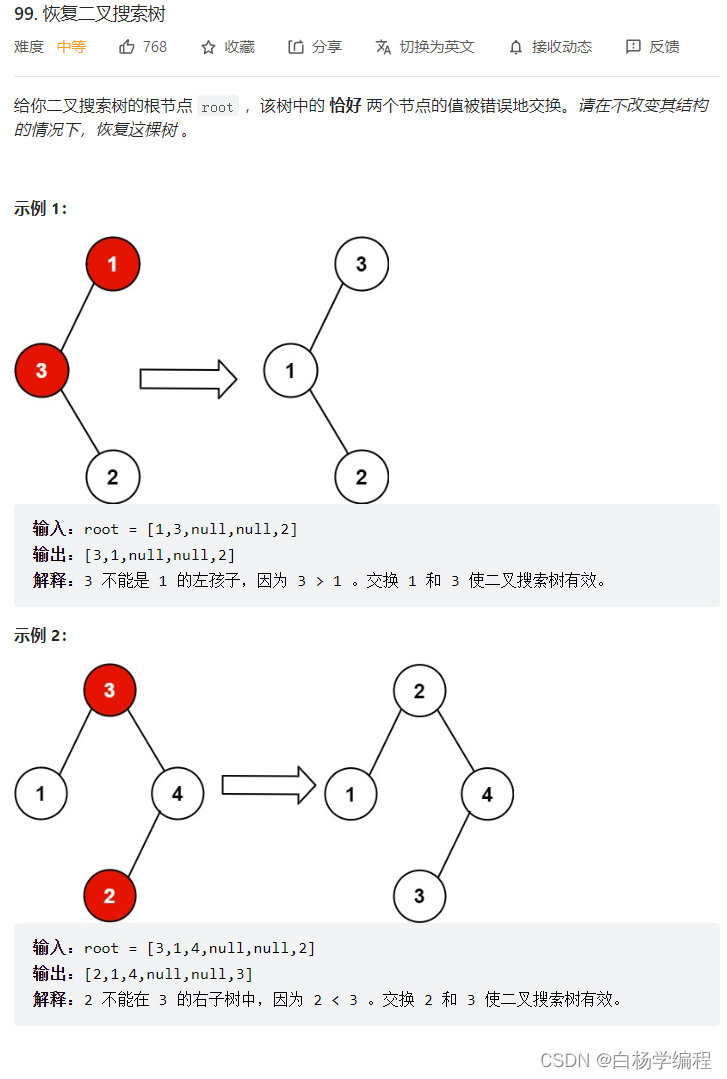
根据二分搜索树的特点，其中序遍历是有序的。

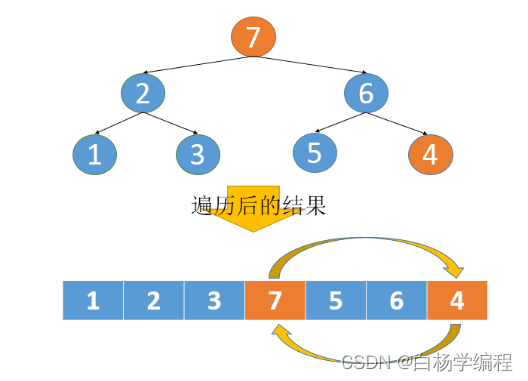
所以先对其进行排序

//中序遍历二叉树
    public void dfs(TreeNode node, List<TreeNode> list){
        if (node.left == null){
            return;
        }
        dfs(node.left,list);
        list.add(node);
        dfs(node.right,list);
    }

然后判断可能错误的节点

public void recoverTree(TreeNode root) {
        List<TreeNode> list = new ArrayList<>();
        dfs(root,list);
        TreeNode x = null;
        TreeNode y = null;
        //打印遍历的结果，遍历可能出现出错的节点 x 和 y
        for (int i = 0; i < list.size() - 1; i++) {
            if (list.get(i).val > list.get(i + 1).val){
                y = list.get(i + 1);
                if (x == null){
                    x = list.get(i);
                }
            }
        }
        //当 x 和 y 不为空是交换节点两个的值，恢复二叉树
        if (x != null && y != null){
            int temp = x.val;
            x.val = y.val;
            y.val = temp;
        }
    }

    //中序遍历二叉树
    public void dfs(TreeNode node, List<TreeNode> list){
        if (node.left == null){
            return;
        }
        dfs(node.left,list);
        list.add(node);
        dfs(node.right,list);
    }

原文地址：https://www.jb51.cc/wenti/3280179.html