1. 旋转向量
可以用一个3*3的向量表示一个旋转变换;
[
a
1
a
2
a
3
]
=
[
e
1
T
e
1
′
e
1
T
e
2
′
e
1
T
e
3
′
e
2
T
e
1
′
e
2
T
e
2
′
e
2
T
e
3
′
e
3
T
e
1
′
e
3
T
e
2
′
e
3
T
e
3
′
]
[
a
1
′
a
2
′
a
3
′
]
=
R
a
′
\begin{bmatrix} a_1 \\ a_2 \\ a_3\end{bmatrix} = \begin{bmatrix} e_1^Te_1' & e_1^Te_2' & e_1^Te_3' \\ e_2^Te_1' & e_2^Te_2' & e_2^Te_3' \\ e_3^Te_1' & e_3^Te_2' & e_3^Te_3'\end{bmatrix}\begin{bmatrix} a_1' \\ a_2' \\ a_3'\end{bmatrix}=Ra' \\
⎣
⎡a1a2a3⎦
⎤=⎣
⎡e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′⎦
⎤⎣
⎡a1′a2′a3′⎦
⎤=Ra′
缺点:
①SO(3)本身有用了9量来表示3个自由度;SE(3)用16个量表示6个自由度;这种表示是冗余的,不够紧凑;
②旋转矩阵和变换矩阵必须是行列式为1的正交矩阵,这个约束导致在估计和优化时难以求解;
2. 旋转向量\轴角
将旋转表示为绕着转轴n旋转角度
θ
\theta
θ的运动,这样用一个三位向量就可以描述旋转;
缺点:存在奇异性,任何
2
n
π
2n\pi
2nπ的旋转在角轴上等于没有旋转;
3. 欧拉角
将一个旋转定义为绕着3个轴的3次旋转(分成3段旋转),按照绕轴旋转的顺序和绕固定轴还是旋转后的轴有多种定义;
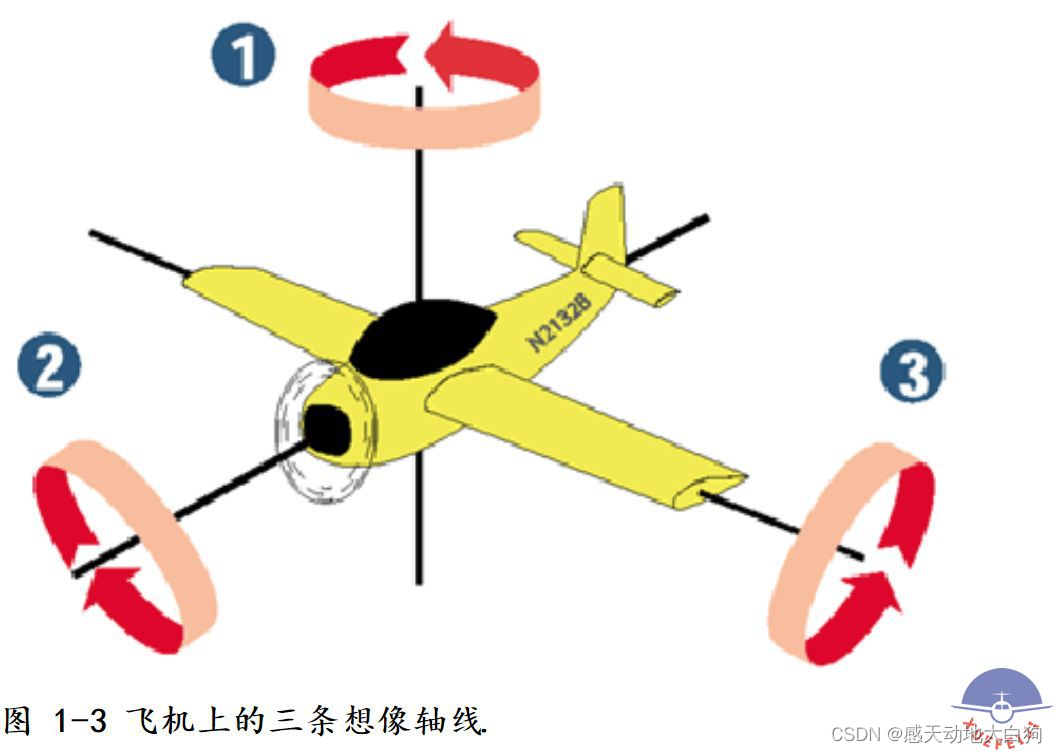
常用的设定为“偏航-俯仰-滚转”(yaw-pitch-roll),你可以想象自己是一架飞机,描述自己的旋转时往往是说:
①我左右转了多少度(绕着z轴,即偏航yaw);
②我上下抬升或下降了多少度(绕着y轴,即俯仰pitch);
③我机体旋转了多少度(绕着x轴,即翻滚roll)
缺点:存在万向锁问题,在特定情况下,旋转后的轴和旋转前的轴重合,使得3次旋转退化成两次旋转,失去了一个自由度;由于这个问题的存在,欧拉角往往只用于方便的可视化,但是如自动驾驶的场景其实也有使用(因为车辆主要关注偏航角yaw)
4. 四元数
旋转矩阵具有冗余性,角轴和欧拉角具有奇异性(3维上的奇异性表示是不存在的);而四元数用1个实部+3个虚部表示旋转,既是紧凑的也没有奇异性;
q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
=
[
s
,
v
]
T
{
i
2
=
j
2
=
k
2
=
−
1
i
j
=
k
,
j
i
=
−
k
j
k
=
i
,
k
j
=
−
i
k
i
=
j
,
i
k
=
−
j
q = q_0 + q_1i + q_2j + q_3k=[s, v]^T \\ \left\{ \begin{array}{lr} i^2 = j^2 = k^2=-1 \\ ij=k, ji=-k \\ jk=i, kj=-i \\ ki=j, ik=-j \end{array} \right.
q=q0+q1i+q2j+q3k=[s,v]T⎩
⎨
⎧i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−js表示实部,v表示虚部,在四元数中
q
q
q和
−
q
-q
−q表示一个相同的旋转
四元数表示旋转的例子:一个点
p
=
[
x
,
y
,
z
]
∈
R
3
p=[x, y, z]\in \mathbb{R}^3
p=[x,y,z]∈R3经过旋转之后编程点
p
′
p'
p′,对应了四元数q,则有p在四元数下的表示以及旋转变化为:
p
=
[
0
,
x
,
y
,
z
]
T
=
[
0
,
v
]
T
p
′
=
q
p
q
−
1
p=[0, x, y, z]^T = [0, v]^T \\ p' = qpq^{-1}
p=[0,x,y,z]T=[0,v]Tp′=qpq−1计算后的四元数
p
′
p'
p′的虚部就是旋转后的坐标;
缺点:不够直观
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




