LeetCode.H32
题目:
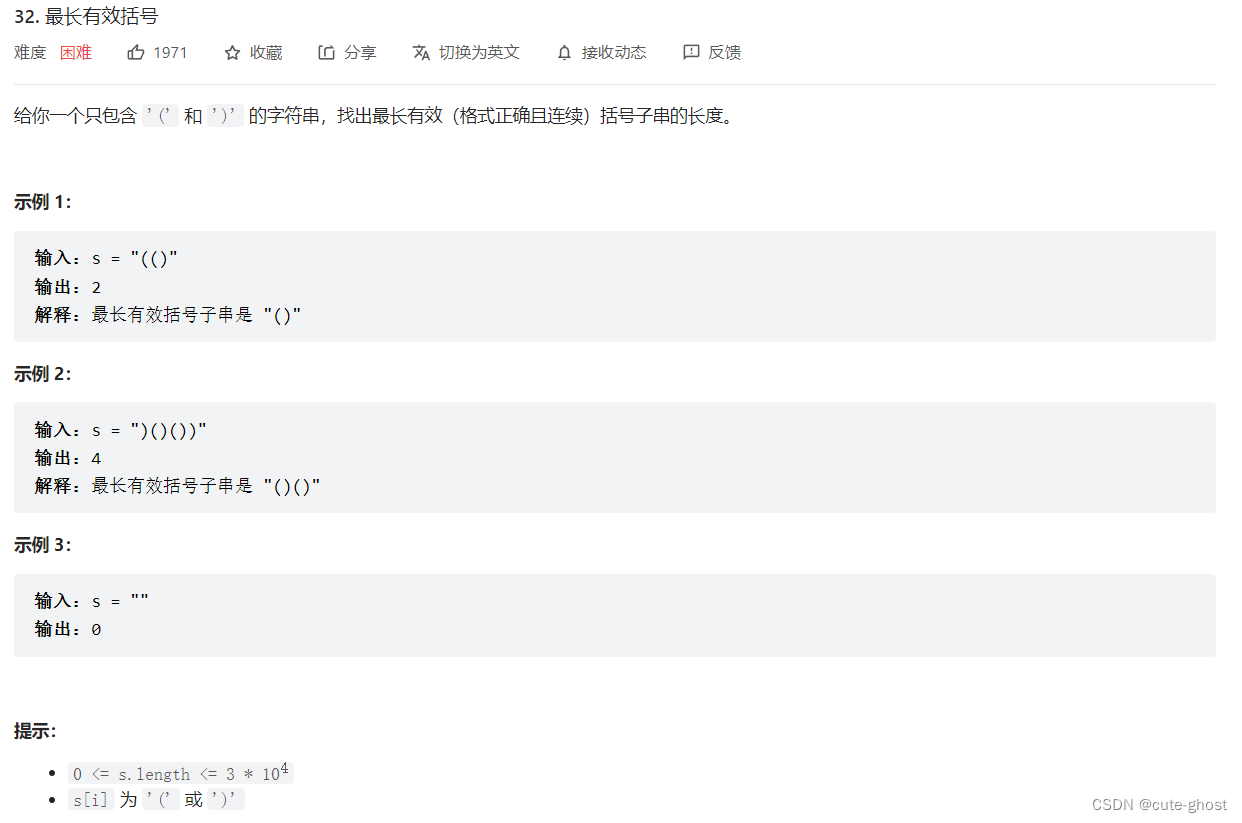
题目大意:
如图所示。
数据范围:
如图所示
一 、解法 :
思路:
dp:定义 f[i] 为以 i 为结尾的连续的最长有效括号的长度。
- 显然如果 s[i] = “(”, 则 f[i] = 0。因为不可能有以 “(” 结尾的有效括号。
- 如果 s[i] = “)”,则需要考虑 s[i - 1] 是什么。
- 如果 s[i - 1] = “(”,则 s[i - 1] 可以与 s[i] 构成一个括号对,则状态转移方程为 f[i] = f[i - 2] + 2。表示以 i 为结尾的最长有效括号长度为由 s[i - 1]、s[i] 组成的括号对 和 在这一个括号对之前的由 以 i - 2 为结尾的最长有效括号长度组成。
- 如果 s[i - 1] = “)”,假设以 i - 1 为结尾的最长有效括号序列为s[k]、s[k + 1] … s[i - 1],其长度为 f[i - 1],如果 s[i] 存在一个 “(” 与它匹配, 那么 s[i] 所匹配的一定是 s[k - 1]的 “(”。
- 所以如果 s[k - 1] = “(”, 及s[i - f[i - 1] - 1] = “(”,那么状态转移方程为 f[i] = f[i - 1] + f[i - f[i - 1] - 2] + 2,其中f[i - 1] 代表了以 i - 1 为结尾的最长有效括号序列s[k]、s[k + 1] … s[i - 1]的长度。则 f[i - f[i - 1] - 2] 代表了在 以 s[k - 1] ( 为一个"(" )、s[k]、s[k + 1] … s[i - 1] 之前的以 s[k - 2] 为结尾的最长有效括号序列长度,2代表了s[k - 1]、和 s[i] 组成的括号对。
初始时 f[i] 都为0,从前向后遍历s。
代码:
class Solution {
public int longestValidParentheses(String s) {
int[] f = new int[s.length()];
int maxlen = 0;
for (int i = 1; i < s.length(); i ++ ){
if (s.charat(i) == ')'){
if (i - 1 >= 0 && s.charat(i - 1) == '(')
f[i] = (i - 2 >= 0 ? f[i - 2] : 0) + 2;
else if (i - f[i - 1] - 1 >= 0 && s.charat(i - f[i - 1] - 1) == '('){
f[i] = f[i - 1] + (i - f[i - 1] - 2 >= 0 ? f[i - f[i - 1] - 2] : 0) + 2;
}
}
maxlen = Math.max(maxlen, f[i]);
}
return maxlen;
}
}
时空复杂度分析等:
- 时间复杂度 : O(n)
- 空间复杂度 : O(n)
二 、解法 :
思路:
栈:具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」,这样的做法主要是考虑了边界条件的处理,栈里其他元素维护左括号的下标:
- 对于遇到的每个 ‘(’ ,我们将它的下标放入栈中。
- 对于遇到的每个 ‘)’ ,我们先弹出栈顶元素表示匹配了当前右括号:
- 如果栈为空,说明当前的右括号为没有被匹配的右括号,我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
- 如果栈不为空,当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
我们从前往后遍历字符串并更新答案即可。
需要注意的是,如果一开始栈为空,第一个字符为左括号的时候我们会将其放入栈中,这样就不满足提及的「最后一个没有被匹配的右括号的下标」,为了保持统一,我们在一开始的时候往栈中放入一个值为 -1 的元素。
代码:
class Solution {
public int longestValidParentheses(String s) {
Deque<Integer> stk = new arraydeque<>();
int maxlen = 0;
stk.push(-1);
for (int i = 0; i < s.length(); i ++ ){
if (s.charat(i) == '('){
stk.push(i);
}else{
stk.pop();
if (!stk.isEmpty()){
maxlen = Math.max(maxlen, i - stk.peek());
}else{
stk.push(i);
}
}
}
return maxlen;
}
}
时空复杂度分析等:
-
时间复杂度 : O(n)
-
空间复杂度 : O(n)
题目链接:
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




