1、什么是计数排序?
计数排序的原理:
计数排序是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第 i 个元素是待排序数组A中值等于 i 的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它适用于一定范围的整数排序。
2、计数排序到底是如何排序的呢?
下面通过一个动图来看一看计数排序到底是怎么样移动的

小花:如果用快速排序,归并排序等这些排序算法的话,那么他们的时间复杂度其实是 O(nlogn)。那么有没有一种方法,使得它的时间复杂度是 O(n) 呢?
小明:答案肯定是有的,我们之前学的排序算法,无论是冒泡排序还是快速排序等等,都是基于元素之间的比较进行排序的。但是现在有一种特殊的排序算法不是基于元素的比较,而是利用数组下标来确定元素的正确位置,这种算法叫做【计数排序】
小花:还是不太明白,数组下标怎么能用来帮助排序呢?能不能具体说说呢?
小明:随机整数的取值范围都有可能是多少呢?
小花:这太简单了,这些整数的值当然在 0,1,2,3,4,5,6,7,8,9,10这 11 个数里面咯
小明:很棒,我们可以根据这个整数取值范围,建立一个长度为11的数组,下标从0到10,元素初始值全为0。
(1)举个例子,假定20个随机整数的值如下,你会如何排序呢?
arr[] = {9,3,5,4,9,1,2,7,8,1,3,6,5,3,4,0,10,9 ,7,9}。
(2)我们可以创建一个数组大小为 11 的临时数组 temp

因为数组的最大值是 10,所以临时数组的最大下标为 10 即可
(3)然后遍历数组,第一个整数是9,那么数组下标为9的元素加1:

(4)第二个整数是3,那么数组下标为3的元素加1:

继续遍历数列并修改数组…
最终,数列遍历完毕时,数组的状态如下:

(5)之后我们只需要遍历临时数组 temp,输出临时数组元素的下标值即可,元素的值是几,就输出几次,结果如下:
0,1,1,2,3,3,3,4,4,5,5,6,7,7,8,9,9,9,9,10
显然,这个输出的数列已经是有序的了。
3、代码实现
public static int[] countSort(int[] arr) {
if(arr == null || arr.length < 2) return arr;
//寻找数组的最大值,该值用来创建临时数组用的
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if(max < arr[i])
max = arr[i];
}
//根据数列最大值创建大小为max + 1的临时数组
int[] temp = new int[max + 1];
//遍历数列,填充统计数组
for (int i = 0; i < arr.length; i++) {
temp[arr[i]]++;
}
//把临时数组统计好的数据汇总到原数组
int index = 0;
for (int i = 0; i <= max; i++) {
// temp[i] 的值表示元素 i 出现的次数
for (int j = temp[i]; j > 0; j--) {
arr[index ++] = i;
}
}
return arr;
}
4、代码优化
小明:从功能角度这段代码可以实现整数的排序。但是这段代码也存在一些问题,你发现了吗?
小花:这太简单了,我们现在只是以数列的最大值来决定统计数组的长度,其实很不严谨,比如下面数列:
95,94,91,98,99,90,99,93,91,92
小花:这个数列的最大值为99,但是最小的整数是90。如果创建长度为100的数组,前面从0到89的空间位置就都浪费了!
小明:很棒,我们不再以(输入数列的最大值+1)作为统计数组的长度,而是以(数列最大值和最小值的差+1)作为统计数组的长度。
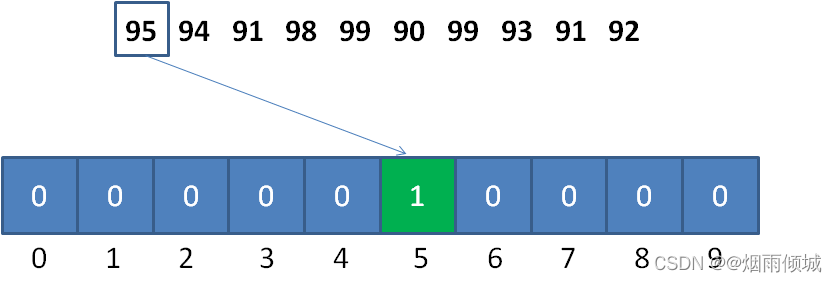
以刚才的数列为例,统计数组的长度为 99-90+1 = 10 ,偏移量等于数列的最小值 90 。所以我们创建大小为10的临时数组就可以了,这样就能大大节省空间浪费。
对于第一个整数95,对应的统计数组下标是 95-90 = 5,如图所示:
public static int[] countSort2(int[] arr) {
if(arr == null || arr.length < 2) return arr;
int min = arr[0];
int max = arr[0];
// 寻找数组的最大值与最小值
for (int i = 1; i < arr.length; i++) {
if(max < arr[i])
max = arr[i];
if(min > arr[i])
min = arr[i];
}
int d = max - min + 1;
//创建大小为max的临时数组
int[] temp = new int[d];
//统计对应元素个数
for (int i = 0; i < arr.length; i++) {
temp[arr[i] - min]++;
}
int k = 0;
//把临时数组统计好的数据汇总到原数组
for (int i = 0; i < d; i++) {
// temp[i] 的值表示元素 i 出现的次数
for (int j = temp[i]; j > 0; j--) {
arr[k++] = i + min;
}
}
return arr;
}
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




