文章目录
- 组合,排列,子集
- [41. 缺失的第一个正数](https://leetcode-cn.com/problems/first-missing-positive/) -两个思路
- [50. Pow(x, n)](https://leetcode-cn.com/problems/powx-n/)
- [58. 最后一个单词的长度](https://leetcode-cn.com/problems/length-of-last-word/)
- [71. 简化路径](https://leetcode-cn.com/problems/simplify-path/)
- [125. 验证回文串](https://leetcode-cn.com/problems/valid-palindrome/)
- [26. 删除有序数组中的重复项](https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/)
组合,排列,子集
给出一个集合[1,2,3,4],输出其:
组合:k=2,[1,2],[1,3],[1,4]…
排列:1234,1243,1324,1342…
子集:[1],[1,2],[1,2,3]…
编写代码时,主要分为两类,
排列顺序需要考虑:排列
road 代表已有轨迹,choice代表选择
每次需要复制,并添加新的选择,choice去除选择
为什么要复制,不用全局数组?
主要在于其中的for循环
road 和 choice 都要参与到下一次循环,而我们希望这轮执行完,和初始一致(有的不需要,比如visited数组,就直接用全局很舒服)
所以 要不就是对road和choice复制后 操作
或者 操作完,把它恢复原状
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
k = len(nums)
result = []
def dfs(road, choice_n):
if len(road) == k:
result.append(road)
return
else:
for num_n in choice_n:
road_new = road[:]
road_new.append(num_n)
choice_new = choice_n[:]
choice_new.remove(num_n)
dfs(road_new, choice_new)
dfs([], nums)
return result
排列顺序不需要考虑:组合,子集
很巧妙的方法,通过for循环开始的位置
保证只能遍历后面的
组合
截至位置为 有k个数
def combine(n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res=[]
def dfs(track,start,choice):
print(f"当前track:{track}")
print(f"当前start:{start}")
if len(track)==k:
res.append(track)
return
else:
# 关键是理解 其中的start,每个节点的选择只能是当前节点后面的
for i in range(start,len(choice)):
num=choice[i]
track_new=track[:]
track_new.append(num)
dfs(track_new,i+1,choice)
dfs([],0,[i+1 for i in range(n)])
return res
子集
每个遍历点都加上
def subsets(nums):
res=[]
def dfs(track,start,choice):
res.append(track)
for i in range(start,len(choice)):
new_track=track[:]
new_track.append(choice[i])
dfs(new_track,i+1,choice)
dfs([],0,nums)
res.remove([])
return res
没有重复数字的子集,组合,排列
首先把初始数组排序一下,然后记录last_num,一样则不添加…第一个赋值成" ",字符串还巧滴.
47. 全排列 II
def permuteUnique(nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
nums=sorted(nums)
print(f"排序后:{nums}")
n=len(nums)
res=[]
def dfs(track,choice):
print(f"track:{track}")
print(f"choice:{choice}")
if len(track)==n:
res.append(track)
return
else:
last_num=" "
for num in choice:
if num == last_num:
continue
last_num=num
new_choice=choice[:]
new_choice.remove(num)
new_track=track[:]
new_track.append(num)
dfs(new_track,new_choice)
dfs([],nums)
return res
if __name__ == '__main__':
nums=[1,1,2]
print(permuteUnique(nums))
41. 缺失的第一个正数 -两个思路
本地存储
它要求常数空间复杂度, 立马想到本地存储,本地存储指的是直接在本数组中存储信息,比如全是正数,那么某一位是负数的时候,就代表这一位被标记了.
```python
def firstMissingPositive(nums):
"""
:type nums: List[int]
:rtype: int
"""
n=len(nums)
# 第一次循环将所有负数全变成n+1
for i in range(len(nums)):
if nums[i] <= 0:
nums[i] = n+1
print(nums)
# 第二次循环将所有>0且<=n的数 对应的索引上的数全变成负数
# 注意索引与该数之间差1哦
# 防止[1,1,1]这种情况,变成负数的时候,要先检查它是否是正数
for i in range(len(nums)):
if abs(nums[i]) <= n and nums[abs(nums[i])-1] >0:
nums[abs(nums[i])-1] = -nums[abs(nums[i])-1]
print(nums)
for i in range(len(nums)):
if nums[i] > 0:
return i+1
return n+1
跳转遍历
指的是o(n)时间复杂度的遍历
需要 能够区分本位置的数对不对
然后立足于本位置,不断交换
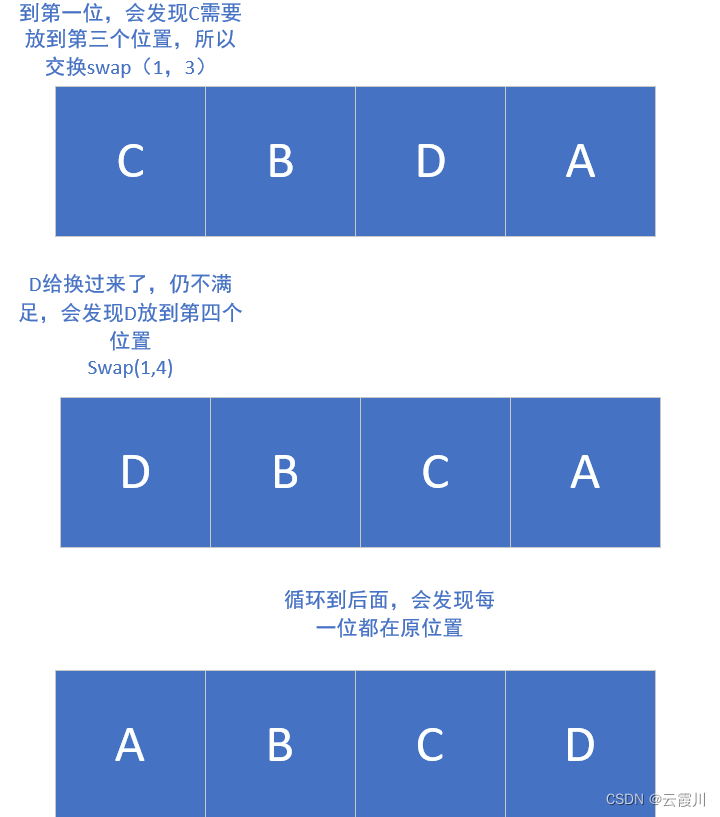
rom typing import List
class Solution:
# 3 应该放在索引为 2 的地方
# 4 应该放在索引为 3 的地方
def firstMissingPositive(self, nums: List[int]) -> int:
size = len(nums)
for i in range(size):
# 先判断这个数字是不是索引,然后判断这个数字是不是放在了正确的地方
while 1 <= nums[i] <= size and nums[i] != nums[nums[i] - 1]:
self.__swap(nums, i, nums[i] - 1)
for i in range(size):
if i + 1 != nums[i]:
return i + 1
return size + 1
def __swap(self, nums, index1, index2):
nums[index1], nums[index2] = nums[index2], nums[index1]
50. Pow(x, n)
记忆化递归
快速幂算法
比如
2
10
=
2
5
∗
2
5
2^{10}=2^5 * 2^5
210=25∗25 只需要算pow(2,5) 即可
利用递归(二分的思路),加上记忆化策略(当函数遇到相同参数时,直接用cache) 语法糖@cache
class Solution:
def myPow(self, x: float, n: int) -> float:
"""
:type x: float
:type n: int
:rtype: float
"""
return dfs(x,n)
@cache
def dfs(x,n):
# 如果是1的话
if n==0:
return 1
if n == 1:
return x
# 如果是2的话
if n==2:
return x*x
if n==-1:
return 1/x
# 如果n是偶数的话
if n%2==0:
return dfs(x,n//2)*dfs(x,n//2)
else: # 如果是奇数的话
return dfs(x,n//2)*dfs(x,n//2)*dfs(x,n%2)
58. 最后一个单词的长度
正则表达式 字符串处理
很多字符串题目可以直接用正则表达式做
这题是最基础那种,连正则表达式都不需要
def lengthOfLastWord(s):
"""
:type s: str
:rtype: int
"""
# api 战士
return len(s.strip().split(" ")[-1])
71. 简化路径
正则表达式+栈
用re.split 轻松分割
用栈,类似括号匹配的思路
遇到… 则弹出一个
import re
class Solution:
def simplifyPath(self, path: str) -> str:
stack1=[]
names=re.split(r'/+',path)
print(names)
for name in names:
if name=='..':
if len(stack1)!=0:
stack1.pop()
elif name=='.' or name=='':
continue
else:
stack1.append(name)
return "/"+"/".join(stack1)
125. 验证回文串
正则表达式
import re
class Solution:
def ispalindrome(self, s: str) -> bool:
a="".join(re.split(r"[^a-zA-Z0-9]+",s)).lower()
if len(a)%2==0:
if a[:len(a)//2]==a[len(a)//2:][::-1]:
return True
if len(a)%2==1:
if a[:len(a)//2]==a[len(a)//2+1:][::-1]:
return True
return False
26. 删除有序数组中的重复项
本地修改-快慢指针
需要在数组原地存储,则用慢指针来存储,快指针用来访问
# 快慢指针
# 慢指针负责存储
# 快指针负责查找
# 当快指针找到一个符合要求的则传给慢指针
def removeDuplicates(nums):
"""
:type nums: List[int]
:rtype: int
"""
slow=0
for fast in range(len(nums)):
if nums[fast] != nums[slow]:
slow+=1
nums[slow]=nums[fast]
return nums[:slow+1]
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




