MATLAB程序设计与应用 3.3 矩阵求值

MATLAB程序设计与应用

3. 第3章 MATLAB矩阵处理

文章目录

- MATLAB程序设计与应用
- - 3. 第3章 MATLAB矩阵处理
  - - 3.3 矩阵求值

3.3 矩阵求值

矩阵求值是指对一个矩阵进行某种运算，其结果是一个数值，包括求矩阵的行列式值、秩、迹、范数、条件数等。

3.3.1 方阵的行列式

把一个方阵看做一个行列式，并对其按行列式的规则求值，这个值就称为矩阵所对应的行列式的值。在 MATLAB中，求方阵A所对应的行列式的值的函数是 det(A)。

>> A = rand(4)

A =

    0.8147    0.6324    0.9575    0.9572
    0.9058    0.0975    0.9649    0.4854
    0.1270    0.2785    0.1576    0.8003
    0.9134    0.5469    0.9706    0.1419

>> B = det(A)

B =

   -0.0261

3.3.2 矩阵的秩和迹

矩阵的秩

矩阵线性无关的行数与列数称为矩阵的秩。

什么是矩阵线性无关的行与列？

===> 一个mxn矩阵A是由m个行向量组成或由n个列向量组成的。通常，对于一组向量x1,x2,…,xp，若存在一组不全为0的数ki(i = 1,2,…,p)使得k1x1 + k2x2 + … + kpxp = 0成立，则称这p个向量线性相关，否则称线性无关。对于mxn 矩阵A,若m个行向量中有r(r≤m)个行向量线性无关，而其余为线性相关，称为矩阵A的行秩；类似地可定义矩阵A的列秩。
矩阵的行秩和列秩必定相等，将行秩和列秩统称为矩阵的秩，有时也称为该矩阵的奇异值数。

在MATLAB中，求矩阵秩的函数是rank(A)。
```
>> A = [2,2,-1,1;4,3,-1,2;8,5,-3,4;3,3,-2,2];
>> r = rank(A)

r =

     4
% A 是一个满秩矩阵
```
矩阵的迹

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。在 MATLAB 中，求矩阵的迹的函数是trace(A)。
```
>> A = [2,2,3;4,5,-6;7,8,9];
>> trace(A)

ans =

    16
```

3.3.3 向量和矩阵的范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。范数有多种方法定义，其定义不同，范数值也就不同，因此，讨论向量和矩阵的范数时，一定要弄清是求哪一种范数。

向量的3种常用范数

设向量V=(v1,v2,…,vn)，它的3种范数定义如下。
- 向量 1-范数：向量元素的绝对值之和。
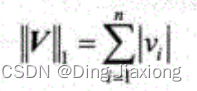
- 向量 2-范数：向量元素平方和的平方根。
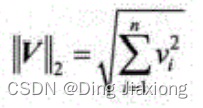
- 向量 ∞-范数：所有向量元素绝对值中的最大值。
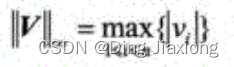
在MATLAB中，求这3种向量范数的函数：
- norm(V , 1)
- norm( V ) 或 norm(V , 2)
- norm(V , inf)
其中V是向量。
```
>> V = [-1,1/2,1];
>> v1 = norm(V,1) % 求V的 1-范数

v1 =

    2.5000

>> v2 = norm(V,2) % 求V的 2-范数

v2 =

    1.5000

>> vinf = norm(V,inf) % 求V的 ∞-范数

vinf =

     1
```
矩阵的范数

设A是一个m×n矩阵，V是一个含有n个元素的列向量，矩阵A的范数可以定义为

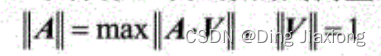
因为A是一个m×n矩阵，而V是一个含有n个元素的列向量，所以A·V是一个含有m个元素的列向量。在前面已经定义了3种不同的向量范数，按照上式也可以定义3种矩阵范数，这样定义的矩阵范数||A||称为A从属于向量的范数。

从属于3种向量范数的矩阵范数计算公式如下。
- 矩阵A的 1-范数：所有矩阵列元素绝对值之和的最大值。
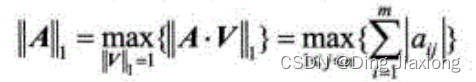
- 矩阵A的 2-范数: A’A矩阵的最大特征值的平方根。
  
  其中，λ1是A’A的最大特征值。
- 矩阵A的 ∞-范数:所有矩阵行元素绝对值之和的最大值。
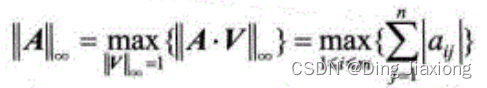
MATLAB提供了求3种矩阵范数的函数。
```
>> A = [1,0,1,0,5;3,5,7,4,6]

A =

     1     0     1     0     5
     3     5     7     4     6

>> a1 = norm(A , 1) % 求A 的 1-范数

a1 =

    11

>> a2 = norm(A , 2) % 求A 的 2-范数

a2 =

   12.1738

>> ainf = norm(A , inf) % 求A 的 ∞-范数

ainf =

    25
```

3.3.4 矩阵的条件数

在求解线性方程组 AX=b时，一般认为，系数矩阵A中个别元素的微小扰动不会引起解向量的很大变化。这样的假设在工程应用中非常重要，因为一般系数矩阵的数据是由实验数据获得的，并非精确值，但与精确值误差不大。由上面的假设可以得出结论:当参与运算的系数与实际精确值误差很小时，所获得的解与问题的准确解误差也很小。遗憾的是，上述假设并非总是正确的。对于有的系数矩阵，个别元素的微小扰动会引起解的很大变化，在计算数学中，称这种矩阵为病态矩阵，而称解不因其系数矩阵的微小扰动而发生大的变化的矩阵为良性矩阵。
当然，良性与病态是相对的，需要一个参数来描述，条件数就是用来描述矩阵的这种性能的个参数。

矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积，即 cond(A)=||A||· ||A^-1||。这样定义的条件数总是大于1的。条件数越接近于1,矩阵的性能越好，反之，矩阵的性能越差。A有3种范数，相应地可以定义3种条件数。在MATLAB中，计算A的3种条件数的函数如下:

cond(A,1):计算A的1-范数下的条件数。
cond(A)或 cond(A,2):计算A的2-范数下的条件数。
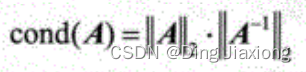
cond(A,inf):计算A的∞-范数下的条件数。

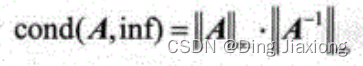
>> A = [2,2,3;4,5,-6;7,8,9];
>> C1 = cond(A)

C1 =

   87.9754

>> B = [2,-5,4;1,5,-2;-1,2,4];
>> C2 = cond(B)

C2 =

    3.7515

矩阵B的条件数比矩阵A的条件数更接近于1，因此，矩阵B的性能要好于矩阵A。

MATLAB程序设计与应用 3.3 矩阵求值