机器学习几种常见凸函数的证明

摘要: 证明几种常见的凸函数.

参考链接: https://zhuanlan.zhihu.com/p/138334587
https://blog.csdn.net/qq_40651017/article/details/105660299

1. 预备知识

1.1 Jacobian 矩阵

假设函数 $F:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 是一个将欧氏 $n$ 维空间映射到欧氏 $m$ 维空间的函数. 该函数由 $m$ 个实函数构成: $y_1(x_1,\dots ,x_n)$, $y_2(x_1,\dots ,x_n)$, $\dots$, $y_m(x_1,\dots ,x_n)$. 这些函数的偏导数组成一个 $m$ 行 $n$ 列的矩阵, 即 Jacobian 矩阵:
$$J_F(x_1,\dots ,x_n)=\left[\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \dots & \frac{\partial y_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \dots & \frac{\partial y_m}{\partial x_n}\end{array}\right]\text{\hspace{1em}(1)}$$

也可以表示为 $\frac{\partial (y_1,\cdots ,y_m)}{\partial (x_1,\cdots ,x_n)}$.
如果 $\mathbf{p}$ 是 ${\mathbb{R}}^n$ 的一个点，函数 $F$ 在 $\mathbf{p}$ 点可微，则 $F$ 在这一点的导数由 $J_F(\mathbf{p})$ 给出.
如果 $m=n$, 则 $J_F(x_1,\dots ,x_n)$ 是一个方阵，其行列式称为 Jacobian 行列式.

1.2 Hessian 矩阵

如果 $f$ 的所有二阶导数都存在, 则 $f$ 的Hessian 矩阵为:
$$H(f)(\mathbf{x})=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}\\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]\text{\hspace{1em}(2)}$$
可以用二阶导数的值判断梯度下降的速率。
注意: 这里的 $f$ 仅仅是一个多元变量的函数, 而不是 1.1 节中的 $F$ 那种多个函数.

1.3 正定矩阵

定义 2. 令 $\mathbf{A}$ 为 $n\times n$ 矩阵. 如果对于任意长度为 $n$ 的非零列向量 $\mathbf{x}$, 均有 ${\mathbf{x}}^{\mathsf{T}}\mathbf{Ax}>0$, 则 $\mathbf{A}$ 为 正定矩阵.
定理 1. $\mathbf{A}$ 正定 $\iff$ $\mathbf{A}$ 的所有特征值为正 $\iff$ $\mathbf{A}$ 的顺序主子式为正.

定义 3. 令 $\mathbf{A}$ 为 $n\times n$ 矩阵. 如果对于任意长度为 $n$ 的非零列向量 $\mathbf{x}$, 均有 ${\mathbf{x}}^{\mathsf{T}}\mathbf{Ax}\ge 0$, 则 $\mathbf{A}$ 为 半正定矩阵.

2. 一元凸函数

定义4. 对于一元函数 $f(x)$, 如果对于任意 $t\in [0,1]$ 均满足:
$$f(t{x}_1+(1-t)x_2)\le tf(x_1)+(1-t)f(x_2),\text{\hspace{1em}(1)}$$
则称 $f(x)$ 为凸函数 (convex function).

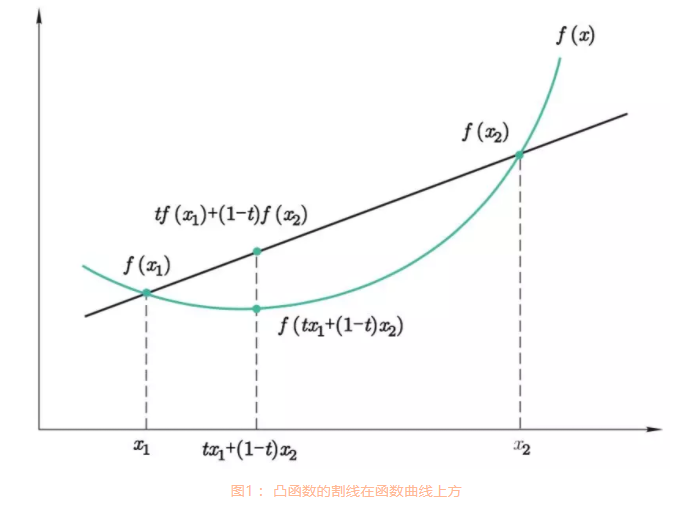
图片来源: https://blog.csdn.net/qq_40651017/article/details/105660299

定理 1. 如果 $f^{\prime \prime }(x)\ge 0$ 恒成立, 则 $f(x)$ 是凸函数.

例 1. $f(x)=x^2$, $f^{\prime }(x)=2x$, $f^{\prime \prime }(x)=2>0$, 因此 $f(x)$ 为凸函数.

结论 1. 多个凸函数的和也是凸函数.
证明: 由函数求导的可加性可知.

3. 多元凸函数

定义5. 如果 $f$ 的 Hessian 矩阵是半正定的，则 $f(X)$ 是凸函数.

4. 几种常用函数

4.1 权值向量的 $l_1$ 范数

令 ${\mathbf{w}}_1=(w_{11},w_{12})$, ${\mathbf{w}}_2=(w_{21},w_{22})$.
$f(t{\mathbf{w}}_1+(1-t){\mathbf{w}}_2)=f(t{w}_{11}+(1-t)w_{21},t{w}_{12}+(1-t)w_{22})=|t{w}_{11}+(1-t)w_{21}|+|t{w}_{12}+(1-t)w_{22}|$

$tf({\mathbf{w}}_1)+(1-t)f({\mathbf{w}}_2)=t|w_{11}|+t|w_{21}|+(1-t)|w_{21}|+(1-t)|w_{22}|$.
前式的某些值如何符号相反会抵消, 如 $w_{11}$ 与 $w_{21}$, 但后者不会. 因此 前式 $\le$ 后式.
得证.

几何解释参见 https://zhuanlan.zhihu.com/p/60236837, 虽然和我理解的有些不同.

4.2 权值向量的 $l_2$ 范数

命题 1. 令 $\mathbf{w}$ 为一个权值向量,
$$f(\mathbf{w})=\Vert \mathbf{w}{\Vert }_2^2\text{\hspace{1em}(2)}$$
是一个凸函数.
证明:
$f(\mathbf{w})={\sum }_{i=1}^m{w}_i^2$,
$H(f)(\mathbf{w})=2{\mathbf{E}}_{m\times m}$ 为单位矩阵的 2 倍, 也为一个正定矩阵, 因此 (2) 为一个凸函数.

4.3 权值矩阵的 F 范数

命题 2. 令 $\mathbf{W}$ 为一个权值矩阵,
$$f(\mathbf{w})=\Vert \mathbf{w}{\Vert }_F^2\text{\hspace{1em}(2)}$$
是一个凸函数.
证明:
与命题 1 的证明同理.

4.4 矩阵的核范数

矩阵 $\mathbf{X}$ 的核范数 $\Vert \mathbf{X}{\Vert }_{\ast }=tr\left(\sqrt{{\mathbf{X}}^{\mathsf{T}}\mathbf{X}}\right)$ 是一个凸函数.
证明: 参见 https://hyper.ai/wiki/2687.
考虑 $\mathbf{X}$ 的奇异值分解 $\mathbf{X}=\mathbf{U}\Sigma {\mathbf{V}}^{\mathsf{T}}$. 同时注意
$$\begin{array}{lll}tr(\sqrt{{\mathbf{X}}^{\mathsf{T}}\mathbf{X}})& =tr(\sqrt{\mathbf{V}{\Sigma }^{\mathsf{T}}{\mathbf{U}}^{\mathsf{T}}\mathbf{U}\Sigma {\mathbf{V}}^{\mathsf{T}}})& \\ & =tr(\sqrt{\mathbf{V}{\Sigma }^{\mathsf{T}}\Sigma {\mathbf{V}}^{\mathsf{T}}})& {\mathbf{U}}^{\mathsf{T}}\mathbf{U}=\mathbf{E}\\ & =tr(\sqrt{\mathbf{V}{\Sigma }^2{\mathbf{V}}^{\mathsf{T}}})& {\Sigma }^{\mathsf{T}}=\Sigma \\ & =tr(\sqrt{\mathbf{V}{\mathbf{V}}^{\mathsf{T}}{\Sigma }^2})& \Sigma 为对角矩阵\\ & =tr(\sqrt{{\Sigma }^2})& \\ & =tr(\Sigma )& \end{array}$$
特别地, 当 $\mathbf{X}$ 为方阵时 $\mathbf{U}=\mathbf{V}$, 这时称为特征值分解.
但是, 我们还无法保证 $tr(\Sigma )\ge 0$.
后面的证明我没看懂, 亟需帮助！