深度优先搜索其实就是在图上找目标点,以起始的点开始,向每个点进行搜索,直到找到目标点。在实际的解题过程中解题过程中,DFS通常是以回溯的考法最多,也最难,后面列出的题目也都是回溯解法居多,这种解法被称为“万能方程式”。
目录
引例
在图上如何寻找从1到8的路径?
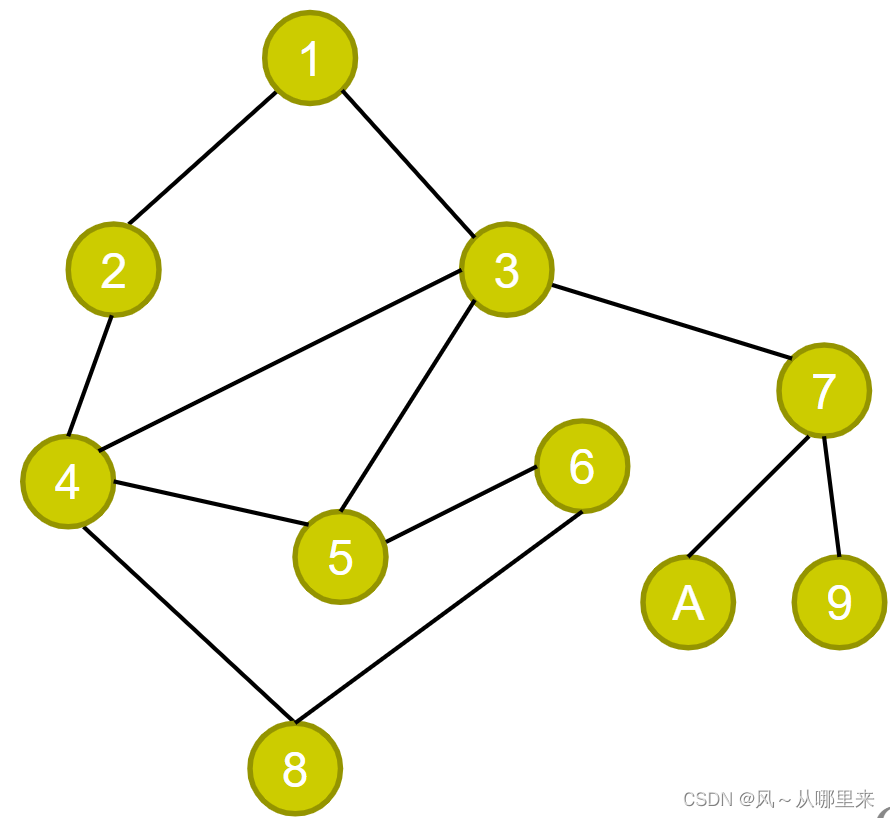
一种策略:只要能发现没走过的点,就走到它。有多个点可走就随便挑一个,如果无路可走就走回退,再看有没有没走过的点可走。
运气最好:1 -> 2 -> 4 -> 8
运气稍差:1 -> 2 -> 4 -> 5 -> 6 -> 8
运气坏:1 -> 3 -> 7 ->9 => 7 -> A => 7 => 3 -> 5 -> 6 -> 8(双线箭头表示回退)
如果是不连通的图,则无法从结点1走到结点8。
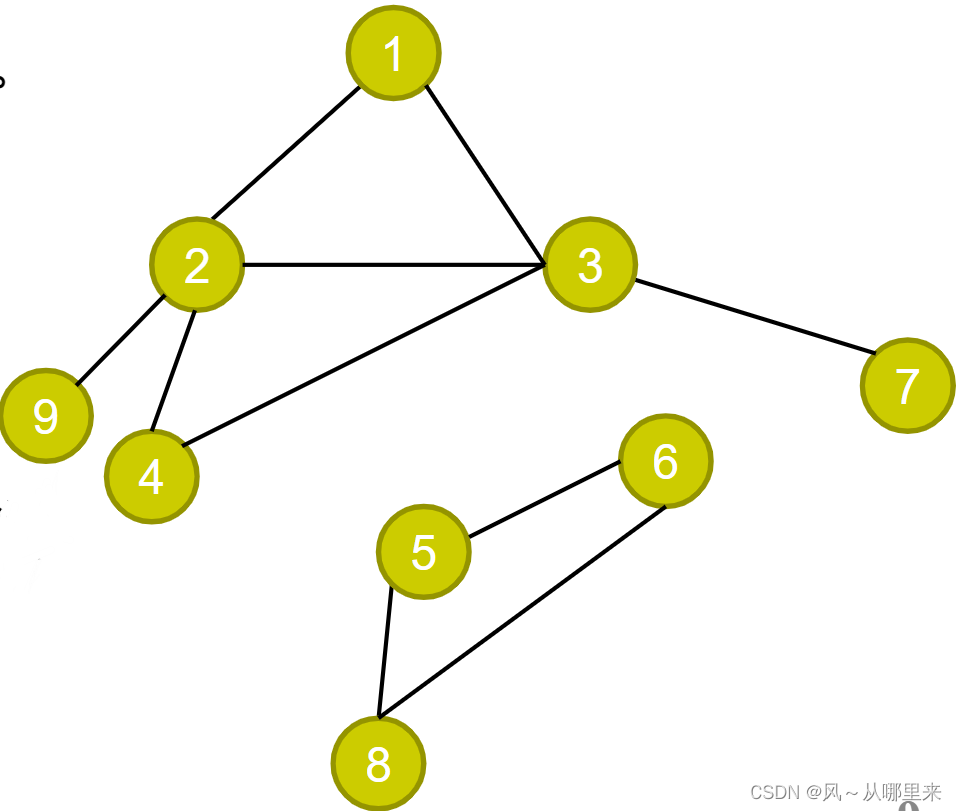
完整的尝试过程可能如下:
1 -> 2 -> 4 -> 3 -> 7 => 3 => 4 => 2 -> 9 => 2 = > 1
结论:不存在从1到8的路径
得出这个结论之前,一定会把从1出发能走到的点全部都走过。
DFS--深度优先搜索(Depth-First-Search)
从起点出发,走过的点要做标记,发现有没走过的点,就随意挑一个往前走,走不了就回退,此种路径搜索策略就称为 “深度优先搜索”,简称 “深搜”。
下面介绍三种解题思路模板:
模板一
判断从V出发是否能走到终点
伪代码如下:
bool Dfs(V){
if(V 为终点)
return true;
if(V 为旧点)
return false;
将V标记为旧点;
对和V相邻的每个结点U{
if(Dfs(U) == true)
return true;
}
return false;
}
int main()
{
将所有点都标记为新点;
起点 = 1;
终点 = 8;
cout << Dfs(起点);
}模板二
判断从V出发是否能走到终点,如果能,要记录路径:
Node path[MAX_LEN];
int depth;
bool Dfs(V){
if(V 为终点){
path[depth] = V;
return true;
}
if(V 为旧点)
return false;
将V标记为旧点;
path[depth] = V;
++depth;
对和V相邻的每个结点U{
if(Dfs(U) == true)
return true;
}
--depth;
return false;
}
int main()
{
将所有点都标记为新点;
depth = 0;
if(Dfs(起点)){
for(int i = 0;i <= depth;++i)
cout << path[i] << endl;
}
}模板三
深度优先遍历图上的所有结点
Dfs(V){
if(V 是旧点)
return;
将V标记为旧点;
对和V相邻的每个点U {
Dfs(U);
}
}
int main(){
将所有点都标记为新点;
while(在图中能找到新点k)
Dfs(k);
}图的表示方法
图的表示方法两种:邻接矩阵和邻接表
邻接矩阵:用一个二维数组G存放图,G[i][j]表示节点i和节点j之间边的情况(如有无边,边方向,权值大小等)。 用该种方式储存图,遍历的时间复杂度为O(),n为节点数目
邻接表:每个节点V对应一个一维数组(vector),里面存放从V连接出去的边,边的信息包括另一顶点,还可能包含边权值等。
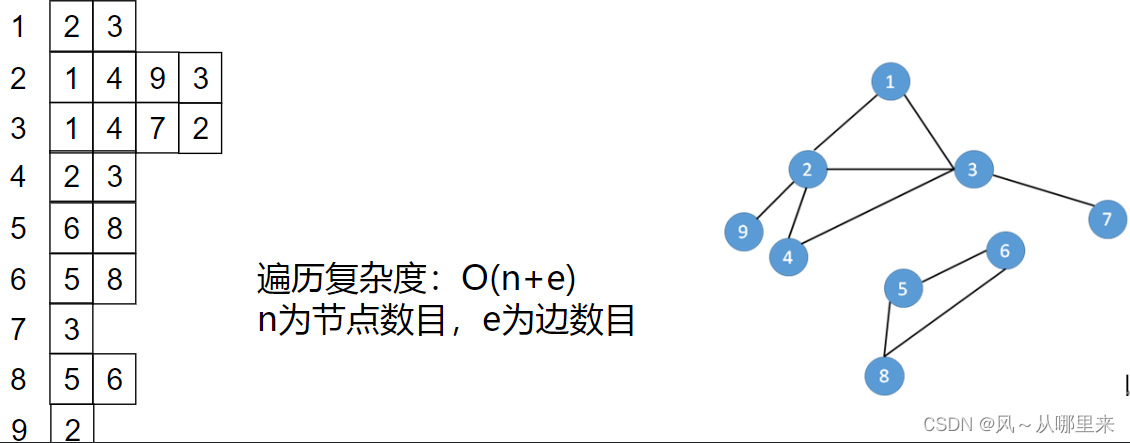
下面是DFS的例题:
城堡问题

输入:
程序从标准输入设备读入数据
第一行是两个整数,分别是南北向,东西向的方块数
在接下来的输入行里,每个方块用一个数字(0 <= p <= 50)描述。用一个数字表示方块周围的墙,1表示西墙,2表示北墙,4表示东墙,8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。
输入的数据保证城堡至少有两个房间。
输出:
城堡的房间数、城堡中最大房间所包括的方块数。
样例输入
4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
样例输出
5
9
看到题目是不是很懵逼,这道题有很多的关键点要想出来。、
首先怎样统计房间的个数,由于我们开始时并不知道每个房间的大小,所以为了方便我们统计房间的个数,我们需要给每个房间“染色”,具体来说就是对于每个房间,DFS,从而给这个房间能够到达的所有位置染色。最后统计一共用了几种颜色,以及每种颜色的数量。比如:
1 1 2 2 3 3 3
1 1 1 2 3 4 3
1 1 1 5 3 5 3
1 5 5 5 5 5 3
从而一共有5个房间,最大的房间(1)占据9个格子。但我们怎么知道那个地方有墙呢,这时就要观察墙的标记,1(西墙)即0001,2(北墙)即0010,4(东墙)即0100,8(南墙)即1000。这样的话,我们就可以用给定的数分别与上每一个墙,即可得到答案。
以此为思路,我们用两个二维数组分别储存房间和染过色标记的房间,那怎样求最大的房间呢,我们选择用一个int型变量来记录。
#include<iostream>
#include<stack>
#include<cstring>
using namespace std;
int R,C;//房间的行列数
int rooms[60][60];//储存房间
int color[60][60];//标记染色过的房间
int maxRoomArea = 0,roomNum = 0;//记录最大房间大小和房间数同时也是染色的标记
int roomArea;//房间的面积
void Dfs(int i,int k){
if(color[i][k])
return;
++roomArea;
color[i][k] = roomNum;
if((rooms[i][k] & 1) == 0)Dfs(i,k - 1);//向西走
if((rooms[i][k] & 2) == 0)Dfs(i - 1,k);//向北走
if((rooms[i][k] & 4) == 0)Dfs(i,k + 1);//向东
if((rooms[i][k] & 8) == 0)Dfs(i + 1,k);//向南
}
int main(){
cin >> R >> C;
for(int i = 1;i <= R; ++i)
for(int k = 1;k <= C; ++k)
cin >> rooms[i][k];
memset(color,0,sizeof(color));//初始化房间的颜色标记为0
for(int i = 1;i <= R; ++i)
for(int k = 1;k <= C; ++k){//以任意一个没有被标记过的位置为起点,DFS搜索房间
if(!color[i][k]){
++roomNum; roomArea = 0;
Dfs(i,k);
maxRoomArea = max(roomArea,maxRoomArea);
}
}
cout << roomNum << endl;
cout << maxRoomArea << endl;
}踩方格
有一个方格矩阵,矩阵边界在无穷远处。我们做如下假设:
a.每走一步时,只能从当前方格运动一格,走到某个方格相邻的方格上;
b.走过的格子立即塌陷无法再走第二次;
c.只能向北、东、西三个方向走;
请问:如果允许在方格矩阵上走n步(n <= 20),共有多少种不同的方案。2种走法只要有一步不一样,即被认为是不同的方案。
改题的思路就是递归,从(i,j)出发,走n步的方案数,等于以下三项之和:
从(i + 1,j)出发,走n - 1步的方案数。前提:(i + 1,j)还没走过
从(i,j + 1)出发,走n - 1步的方案数。前提:(i,j + 1)还没走过
从(i ,j - 1)出发,走n - 1步的方案数。前提:(i,j - 1)还没走过
#include<iostream>
#include<cstring>
using namespace std;
int visited[30][50];
int ways(int i,int j,int n){
if(n == 0)
return 1;
visited[i][j] = 1;
int num = 0;
if(!visited[i][j - 1])
num += ways(i,j - 1,n - 1);
if(!visited[i][j + 1])
num += ways(i,j + 1,n - 1);
if(!visited[i + 1][j])
num += ways(i + 1,j,n - 1);
visited[i][j] = 0;//回溯
return num;
}
int main()
{
int n;
cin >> n;
memset(visited,0,sizeof(visited));//初始化数组
cout << ways(0,25,n) << endl;//由于取数组为50列,所以取中间列开始走
return 0;
}该解题方法中涉及到思想回溯,即当走到某点后重新回到上一个点,将走过的点重置。
Roads
N个城市以数字1命名...N 与单向道路相连。每条道路都有两个与之相关的参数:道路长度和需要为道路支付的通行费(以硬币数量表示)。
鲍勃和爱丽丝曾经住在城市1。在注意到爱丽丝在他们喜欢玩的纸牌游戏中作弊后,鲍勃和她分手了,并决定搬走 - 搬到城市N。他想尽快到达那里,但他缺乏现金。
我们想帮助鲍勃找到从城市1到城市N的最短路径,他可以用他拥有的钱买得起。
输入:
输入的第一行包含整数 K,0 <= K <= 10000,这是 Bob 在途中可以花费的最大硬币数。
第二行包含整数 N,2 <= N <= 100,即城市总数。
第三行包含整数 R,1 <= R <= 10000,即道路总数。
以下每条 R 行通过指定由单个空白字符分隔的整数 S、D、L 和 T 来描述一条道路:
- S 是源城市,1 < = S < = N
- D 是目的地城市,1 < = D < = N
- L 是道路长度,1 < = L < = 100
- T 是通行费(以硬币数量表示),0 <= T <=100
请注意,不同的道路可能具有相同的源城市和目标城市。
输出:
输出的第一行也是唯一一行应包含从城市 1 到总通行费小于或等于 K 硬币的城市 N 的最短路径的总长度。
如果此类路径不存在,则只应将数字 -1 写入输出。
这道题的思路整体来说就是从城市1开始深度优先遍历整个图,找到所有能够到达N的走法,选择一个最优的。
我们这里用邻接表来储存图,结构体Road中 d 表示到达的目的城市,L表示道路长度,t表示路费。在递归中不断地搜索,直到找到最小的路径。
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
int K,N,R;
struct Road{
int d,L,t;
};
vector<vector<Road> > G(110);//邻接表存图
int minLen;
int totalLen;
int totalCost;
int visited[110];
void dfs(int s)
{
if(s == N){
minLen = min(minLen,totalLen);//当遍历一次后,比较最小路径
return;
}
for(int i = 0;i < G[s].size();++i){
Road r = G[s][i];
if(totalCost + r.t > K)//如果花费大于所拥有的钱
continue;
if(!visited[r.d]){//如果该地没走过
totalLen += r.L;
totalCost += r.t;
visited[r.d] = 1;
dfs(r.d);
visited[r.d] = 0;//回溯,即访问过的点初始化,便于下一个点的搜索
totalLen -= r.L;
totalCost -= r.t;
}
}
}
int main()
{
cin >> K >> N >> R;
for(int i = 0;i < R;i++){
int s;
Road r;
cin >> s >> r.d >> r.L >> r.t;
if(s != r.d){ // 当出发地不等于目的地
G[s].push_back(r);//存入邻接表
}
}
memset(visited,0,sizeof(visited));//初始化访问过的数组为0
totalLen = 0; // 总长度
minLen = 1 << 30;//最小路径
totalCost = 0;//总花费
visited[1] = 1;//起始点标记
dfs(1);//递归
if(minLen < (1 << 30)){//有最小路径
cout << minLen << endl;
}
else
cout << "-1" << endl;
return 0;
}
当然我们可以对该算法进行减枝,进而进一步优化代码,我们可以发现如果当前的搜索到的路径大于已经存在的最小路径时,这时就可以直接结束搜索。
if(totalLen + r.L >= minLen)//最优性减枝
continue;如果想进一步进行减枝,我们可以考虑花费的问题,即如果花费相同且走到同样地点时已走总路径大于上一次记录的路径时,这时就没必要再进行下去了,可以直接减枝。当然这样需要再开一个数组,是空间换去时间的方法。
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
int K,N,R;
struct Road{
int d,L,t;
};
vector<vector<Road> > G(110);//邻接表存图
int minL[110][10010];
int minLen;//目前为止最优路径长度
int totalLen;
int totalCost;
int visited[110];
void dfs(int s)
{
if(s == N){
minLen = min(minLen,totalLen);
return;
}
for(int i = 0;i < G[s].size();++i){
Road r = G[s][i];
if(totalCost + r.t > K) // 可行性减枝
continue;
if(!visited[r.d]){
if(totalLen + r.L >= minLen)//最优性减枝
continue;
if(totalLen + r.L >= minL[r.d][totalCost + r.t])//保存中间计算结果,减枝
continue;
minL[r.d][totalCost + r.t] = totalLen + r.L;
totalLen += r.L;
totalCost += r.t;
visited[r.d] = 1;
dfs(r.d);
visited[r.d] = 0;
totalLen -= r.L;
totalCost -= r.t;
}
}
}
int main()
{
cin >> K >> N >> R;
for(int i = 0;i < R;i++){
int s;
Road r;
cin >> s >> r.d >> r.L >> r.t;
if(s != r.d){
G[s].push_back(r);
}
}
memset(visited,0,sizeof(visited));
totalLen = 0;
minLen = 1 << 30;
totalCost = 0;
visited[1] = 1;
for(int i = 0;i < 110;i++){
for(int j = 0;j < 10010;j++)
minL[i][j] = 1 << 30;
}
dfs(1);
if(minLen < (1 << 30)){
cout << minLen << endl;
}
else
cout << "-1" << endl;
return 0;
}
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




